传统上,法学研究者研究法律,大多从法律文本、法律沿革、法律比较等角度着手,但坦白地说,进行定量分析的十分稀缺。法律经济学率先引入了定量分析,为法学研究打开了一个新的领域,但从数理逻辑角度来研究法律的,鲜有人涉足。在我国刑法学界,周详教授是“数理刑法学”研究的倡导者,他认为数理逻辑思维工具是发现、创造、论证刑法问题、原理、体系、知识形态的总发动机,中国刑法学要得到真正的发展,必须先学习并最终掌握数理逻辑思维工具[1]。
本文尝试用数理逻辑来分析、研究法律——如果要给出一个领域归属,可暂将其划归至法律逻辑学领域。本文的研究对象为继承公证,研究范围限定在法定继承,讨论范围仅针对夫妻均为被继承人且夫妻遗产财产所包含的财产完全为夫妻共有财产的情形。作为例证,本文的推理和论证以法定第一顺序继承人继承为例,但为了论证的普适性,有意引入了转继承和代位继承的情形。
把数理逻辑引入法定继承,就需要对相关概念、术语进行逻辑解析和符号表达。为了简化,本文中使用的符号是作者自定义的,系由相关概念、名词的英文单词缩写而成。为了将来便于计算机系统进行智能运算处理,文中引入集合①、继承系数、继承值等概念和表达式,用符号来表达继承中的相关概念,并用公式和推演来展示继承过程,论证夫妻作为被继承人其共有财产遗产在法定继承时混同继承与相互继承的等效性原理成立的条件。希望本篇论文,可以为法学研究者开辟出一个法律逻辑解析的新方向。
一、符号定义
(一)符号及指代的术语。
(1)SS:法定继承;(2)P:财产 ;(3)L:遗产;(4)D:被继承人;(5)SU:继承人;(6)S:配偶;(7)H:丈夫;(8)W:妻子;(9)C:子女;(10)PS:父母;(11)F:父;(12)M:母;(13)BS:兄弟姐妹;(14)HS:夫的配偶;(15)HC:夫的子女;(16)HF:夫的父亲;(17)HM:夫的母亲;(18)HBS:夫的兄弟姐妹;(19)WC:妻的子女;(20)WF:妻的父亲;(21)WM:妻的母亲;(22)WBS:妻的兄弟姐妹;(23)WMF:妻的外祖父;(24)WMM:妻的外祖母……
以上,除了SS主要指代法定继承术语以外,其他符号项都可视为是相应元素的集合,当该项不存在时,该项所代表的集合为空集∅,在运算时其取值等于数值0。比如,当S=0时,表示无配偶或者配偶已离婚或者已死亡,当C=0时,表示无子女,或者子女已死亡。
如果纯粹从遗产的价值出发,为了便于运算,我们设定遗产L的价值符号为△。相应的,H的遗产价值为△H,W的遗产价值为△W。
(二)有关符号和集合的比较解析。
1.死亡时间的比较。
Dt表示死亡时间,DtD表示被继承人的死亡时间,DtSU表示某个继承人的死亡时间;
若DtSU-DtD<0,表示某个继承人先于被继承人死亡,先死亡的是子女时,出现代位继承;若dtsu-dtd>0,表示某个继承人后于被继承人死亡,出现转继承;若DtSU-DtD=0,则表示某个继承人与被继承人同时死亡。
2.子女集合解析。
C代表子女集合,假定该集合中有i个元素, i为0或者≦m的正整数,即0≤i≤m,其中0≤e≤m,则Ci={C0、C1、C2、…、Ce、…、Cm}。当i=0时,Ci为∅,Ci=C0=0
Cc代表某个子女Ce的子女集合(即被继承人的孙子女、外孙子女),假定该集合中有j个元素, j为0或者≤n的正整数,即0≤j≤n,则Ccj={Cc0、Cc1、Cc2、…、Ccn}。当j=0时,Ccj为∅,Ccj=Cc0=0
3.兄弟姐妹集合解析。
BS代表兄弟姐妹集合,假定该集合中有k个元素, k为0或者≤u的正整数,即0≤k≤u,则BSk={BS0、BS1、BS2、…、BSu}。当k=0时,BSk为∅,BSk=BS0=0
4.被继承人、继承人集合解析。
D代表被继承人集合,假定该集合中有λ个元素,λ为0或者≤v的正整数,即0≤λ≤v,则Dλ={D0、D1、D2、…、Dv}。当λ=0时,Dλ为∅,Dλ=D0=0,此时无被继承人;当λ=1时,常见的是D={H}或者D={W};当λ=2时,常见的是D={H、W},也即本文讨论的情形。
以下注意,本文是针对夫妻作为被继承人展开讨论的,为了简化,把DH简写为H,把DW简写为W,但读者应当切记,此时的H、W定位均是被继承人角色,不是一般的继承人。
SU代表继承人集合,假定该集合中有τ个元素,τ为0或者≤w的正整数,即0≦τ≦w,则SUτ={SU0、SU1、SU2、…、SUw}。当τ=0时,SUτ为∅,SUτ=SU0=0,此时无继承人。
5.继承系数和继承值。
本文提出至关重要的一个概念——继承系数,即继承人对被继承人遗产是否继承及继承份额多少的一项量化的、可计算的数值。继承系数用符号q代表。
q的取值范围为0到1之间的自然数,即0≤q≤1。当q=0时,表示不继承,即放弃继承;当0<q<1时,表示继承且部分继承;当q=1时,表示继承且全部继承。
显然,存在如下推论(推论1):对某个被继承人来讲,其所有继承人对该被继承人遗产的继承系数之和为1,即
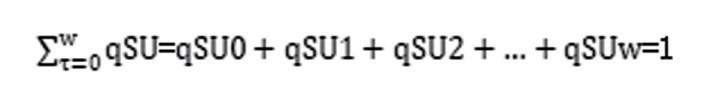
本文提出另一个重要概念——继承值,即某个继承人对某个被继承人的遗产通过继承取得的价值就是继承值。继承值用符号Q代表。
Q的取值范围为0到△之间的数值,即0≤Q≤△。当Q=0时,表示不继承,即放弃继承;当0<Q<△时,表示继承且部分继承;当Q=△时,表示继承且全部继承。
显然,存在如下推论(推论2):某个继承人对某个被继承人遗产的继承值等于该继承人的继承系数与被继承人遗产总价值的乘积,即QSU=△SU=q×△
同样,存在如下推论(推论3):所有继承人对某个被继承人遗产的继承值之和等于各继承人的继承系数与被继承人遗产价值的乘积之和,该和等于被继承人遗产的总价值。即
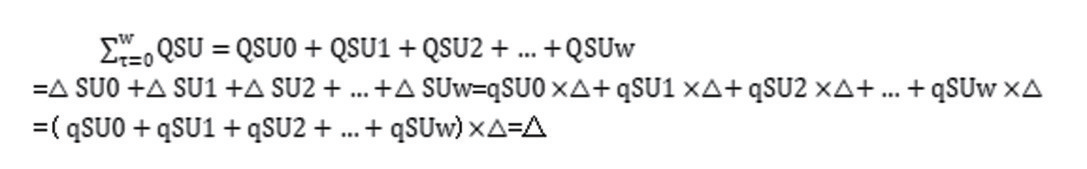
对于被继承人夫妻共有财产遗产△的继承,为了简化表达式,我们将对H的继承值简写为QH,对W的继承值简写为QW。
二、夫妻均作为被继承人时的假定条件及对应的遗产、被继承人、继承人集合解析
假定条件如下:
1.有一对夫妻,丈夫H和妻子W,均已死亡,两人生前财产共同共有,即L=P=△,△=△H+△W。
2.丈夫先死亡,妻子后死亡,即DtH-DtW<0。
3.两人有i个子女,即Ci={C0、C1、C2、…、Ce…、Cm};
3.1.其中,某个子女Ce先于H和W死亡,即DtCe-DtH<0,DtCe-DtW<0,此时存在Ce子女的代位继承,为了简化,我们只考虑Ce直系子女一辈的代位继承;
3.2.其中,Ce有j个子女,即Ccj={Cc0、Cc1、Cc2、…、Ccn}。
4.H的父HF和母HM均先于H死亡,即DtHF-DtH<0,DtHM-DtH<0,此时取值计算时HF=0,HM=0。
5.W的父WF先于W死亡,即DtWF-DtW<0,此时取值计算时wf=0,而w的母wm后于w死亡,即dtwm-dtw>0,此时存在WM的转继承;
5.1其中,WM的父母均先于WM死亡,即WMF=0,WMM=0;
5.2其中,WM有k+1个子女,即W有k个兄弟姐妹,即WBSk={WBS0、WBS1、WBS2、…、WBSu}。
在混同继承时D={H、W},L=P=△。在对H、W遗产分别继承时DH={H}, DW={W}, LH=PH=△H, LW=PW=△W。显然,根据前述假定条件,必然存在LH+LW=△H+△W=△=L。
三、夫妻共有财产遗产混同继承推论展示
此处,我们把H、W两人财产混同为一个整体视作遗产L,但为了展示W方母亲的转继承,有意区分其他继承人对H、W各自遗产的继承过程,但不考虑W对H遗产的继承和转继承,或者说H、W相互不继承。
已知条件,即前文“二”中的假定条件。则QSU(混同)=QH+QW
其中,QH是不含W的H的其他继承人对H的继承值的取值过程,根据推论2展开表达,则
QH={QHCi+QHF+QHM}={QHCi+0+0}={QH{C0、C1、C2、…、Ce、…、Cm}}={QHC0+QHC1+QHC2+…+QHCcj+…+QHCm}={QHC0+QHC1+QHC2+…+QH{Cc0、Cc1、Cc2、…、Ccn}+…+QHCm}={QHC0+QHC1+QHC2+…+QHCc0+QHCc1+QHCc2+…+QHCcn+…+QHCm}={qHC0×△H+qHC1×△H+qHC2×△H+…+qHCc0×△H+qHCc1×△H+qHCc2×△H+…+qHCcn×△H+…+qHCm×△H}=(qHC0+qHC1+qHC2+…+qHCc0+qHCc1+qHCc2+…+qHCcn+…+qHCm)×△H(展开式1)
同样,QW是不含H的W的其他继承人对W的继承值的取值过程,根据推论2展开表达,展开过程同上,省略部分展开步骤,则
QW={QWCi+QWF+QWM}={QWCi+0+QWM}={QW{C0、C1、C2、…、Ce、…、Cm}+QWM}={QWC0+QWC1+QWC2+…+QWCcj+…+QWCm+Q{WMF、WMM、WBSk}}={QWC0+QWC1+QWC2+…+QW{Cc0、Cc1、Cc2、…、Ccn}+…+QWCm+{0+0+Q{WBS0、WBS1、WBS2、…、WBSu}}}=(qWC0+qWC1+qWC2+…+qWCc0+qWCc1+qWCc2+…+qWCcn+…qWCm+qWBS0+qWBS1+qWBS2+…+qWBSu)×△W(展开式2)
带入展开式1和展开式2,则有
QSU(混同)=(qHC0+qHC1+qHC2+…+qHCc0+qHCc1+qHCc2+…+qHCcn+…+qHCm)×△H+(qWC0+qWC1+qWC2+…+qWCc0+qWCc1+qWCc2+…+qWCcn+…+qWCm+qWBS0+qWBS1+qWBS2+…+qWBSu)×△W (展开式3)
根据推论1,则QSU(混同)=1×△H+1×△W=△H+△W=△(等式1)
四、夫妻共有财产遗产相互继承推论展示
此处,我们把H、W的遗产按照相互继承进行展示,即W也继承H的遗产。同前,为了展示W方母亲的转继承,仍然区分其他继承人对H、W各自遗产的继承过程,只是把W对H遗产的继承过程也加入其中,即考虑W对H遗产的继承和转继承。
已知条件与“三”完全一致,即前文“二”中的假定条件。则
QSU(相互)=QH′+QW′=△H′+△W′ 注意,△H′≠△H,△W′≠△W
这里,QH′是相互继承时剔除配偶W对H的继承值△T后其他继承人对H的继承值△H′, QH是混同继承时不含配偶W的其他继承人对H的继承值△H, QHS是相互继承时配偶W对H的继承值△T;QW′是相互继承时把配偶W对H的继承值△T加入到W原遗产△W后其他继承人对W合并后遗产集合即{△W+△T}的继承值△W′,QW是混同继承时其他继承人对W原有遗产的继承值△W, Q{QHS}是相互继承时其他继承人对配偶W对H的继承值的继承值。因为配偶W对H的继承值就是△T,那么其他继承人对配偶W对H的继承值的继承值还是△T。所以,
显然存在Q{QHS}=QHS=△HS=△T,存在△H′=△H-△T,存在 △W′=△W+△T
则QH′=△H′=QH-QHS=△H-△T QW′=△W′=QW+Q{QHS}=△W+△HS=△W+△T
下面,再从另一个角度,用继承系数、继承值的展开式来推演一下QHS 、QH′和QW′。假定,混同继承时,不含W其他继承人对H的继承系数以q标识;相互继承时,W及其他继承人对H的继承系数以q′标识,其他继承人对W的继承系数以q″标识。注意,q′≠q,q″≠q′。
则QHS= q′HS×△H=△T
直接引用“三”对QH的展开式1,则QH′=△H′=QH-QHS
=(qHC0+qHC1+qHC2+…+qHCc0+qHCc1+qHCc2+…+qHCcn+…+qHCm)×△H -q′HS×△H(展开式4)
直接参照“三”对QW的展开式2但用q″来推演Q{QHS}和QW′。
则:Q{QHS}=(q″WC0+q″WC1+q″WC2+…+q″WCc0+q″WCc1+q″WCc2+…+q″WCcn+…+q″WCm+q″WBS0+q″WBS1+q″WBS2+…+q″WBSu)×q′HS×△H(展开式5)
带入展开式2和展开式5,则QW′=△W′=QW+Q{QHS}
=(qWC0+qWC1+qWC2+…+qWCc0+qWCc1+qWCc2+…+qWCcn+…+qWCm+qWBS0+qWBS1+qWBS2+…+qWBSu)×△W +(q″WC0+q″WC1+q″WC2+…+q″WCc0+q″WCc1+q″WCc2+…+q″WCcn+…+q″WCm+q″WBS0+q″WBS1+q″WBS2+…+q″WBSu)×q′HS×△H(展开式6)
带入前面QH′的展开式4和QW′的展开式6,并根据推论1,
则QSU(相互)=QH′+QW′=1×△H -q′HS×△H+1×△W+1×q′HS×△H
=△H -q′HS*△H+△W+q′HS×△H=△H-△T+△W+△T=△H+△W
即,存在QSU(相互)=△H+△W=△(等式2)
五、结论——夫妻作为被继承人其共有财产遗产混同继承与相互继承的等效性及其成立条件
前面“三”推演的结果得到等式1,前面“四”推演的结果得到等式2。
比较等式1和等式2,
因为QSU(混同)=△H+△W=△,QSU(相互)=△H+△W=△,所以QSU(混同)=QSU(相互),或者说,QSU(混同)≡QSU(相互),即QSU(混同)等价于QSU(相互)。
综上,在前面“二”夫妻均作为被继承人H先于W死亡和其他假定条件下,继承人对H、W共有财产遗产的继承,混同继承的结果与相互继承的结果是等价的,或者说混同继承与相互继承的结果是等效的。
不过,为了考虑单独的某个继承人,比较其在混同继承和相互继承时的继承结果的异同,有必要做进一步的推演论证。
设任意一个继承人为SUx,混同继承时其对H的继承系数表示为qHSUx,其对W的继承系数表示为qWSUx;相互继承时其对H的继承系数表示为q′HSUx,其对W的继承系数表示为q″WSUx。
根据推论2,有QSUx=△SUx=qSUx×△
在混同继承时,QSUx(混同)=QHSUx+QWSUx =qHSUx×△H+qWSUx×△W(展开式7)
在相互继承时,QSUx(相互)=Q H′SUx+QW′SUx=q′HSUx×△H′+q″WSUx×△W′
=q′HSUx×(△H-△T)+q″WSUx×(△W+△T)(展开式8)
前面已经述及,通常情况下,无论是混同继承还是相互继承,任意一个继承人SUx的继承意向如果确定不变,那么其对某个被继承人的继承系数就固定不变,即其对H的继承系数不变,其对W的继承系数也不变。这里,我们先考虑SUx对H的继承系数和对W的继承系数不一致时的情形。此时,存在q′HSUx=qHSUx和q″WSUx=qWSUx
把这两个等式和展开式7带入展开式8,则展开式8变成
QSUx(相互)=qHSUx×(△H-△T)+qWSUx×(△W+△T)
=qHSUx×△H+qWSUx×△W+(qWSUx-qHSUx)×△T=QSUx(混同)+(qWSUx-qHSUx)×△T(展开式9)
其中qWSUx-qHSUx是任意一个继承人SUx对W的继承系数和对H的继承系数之差。
设△q=qWSUx-qHSUx,则展开式9转换成
QSUx(相互)=QSUx(混同)+△q×△T(等式3)
对等式3我们可以作进一步解析。
在相互继承时,只要H有遗产△H,则必然存在△T>0。那么,当△q>0时,△q×△T为正,QSUx(相互)>QSUx(混同);当△q<0时,△q×△T为负,QSUx(相互)<QSUx(混同);
当△q=0时,△q×△T=0,QSUx(相互)=QSUx(混同)
综上,我们可以得出如下两个推论:在H(同样还有W)的个人遗产价值>0的前提下,当任意一个继承人SUx对W的继承系数和对H的继承系数不一致的时候,其混同继承和相互继承的结果的确不同(推论4);当任意一个继承人SUx对W的继承系数和对H的继承系数完全一致的时候,混同继承和相互继承的结果对其是等效的(推论5)。